
(a)
The sketch of wave functions and probability density for
(a)
Answer to Problem 17P
The sketch of wave functions and probability density for
Explanation of Solution
The sketch of wave function is plotted below.
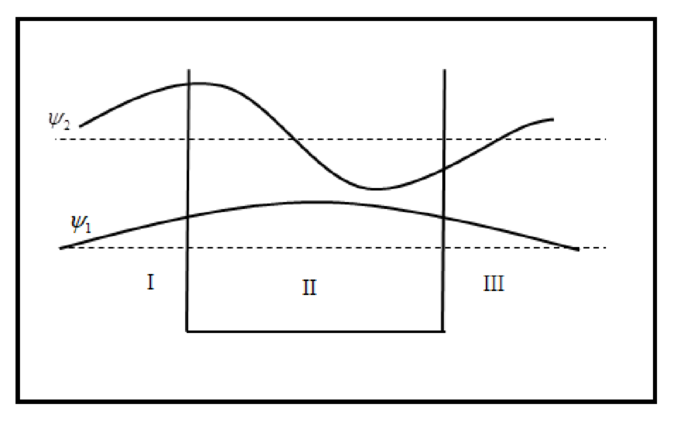
The sketch of probability density is plotted below.
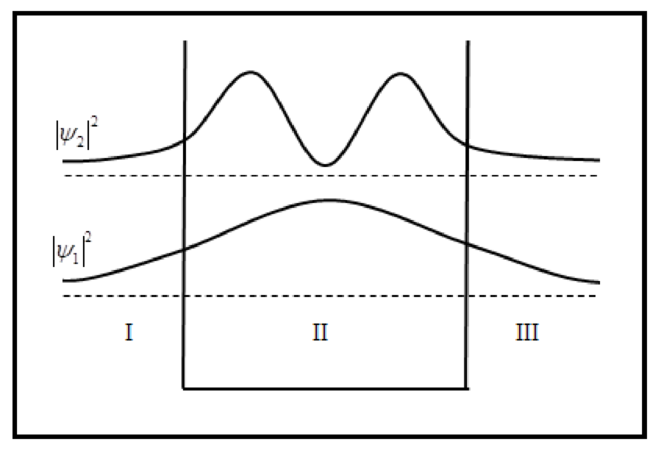
Conclusion:
The sketch of wave functions and probability density for
(b)
The probability of finding the electron between 0.15 nm and 0.35 nm for
(b)
Answer to Problem 17P
The probability of finding the electron for
Explanation of Solution
Write the expression for wave function.
Here,
Write the expression for probability.
Conclusion:
Substitute
Substitute
Thus, the probability of finding the electron for
(c)
The probability of finding the electron between 0.15 nm and 0.35 nm for
(c)
Answer to Problem 17P
The probability of finding the electron for
Explanation of Solution
Conclusion:
Substitute
Substitute
Thus, the probability of finding the electron for
(d)
The energies in electron volts for
(d)
Answer to Problem 17P
The energy for
Explanation of Solution
Write the expression for energy of particle.
Here,
Conclusion:
Substitute
Substitute
Thus, the energy for
Want to see more full solutions like this?
Chapter 6 Solutions
Modern Physics
- A 40 eV atom of mass M1 strikes a lattice atom of mass M2 = 2M1. What is the probability that the lattice atom is displaced? Assume hard-sphere scattering and displacement energy of 25 eV.arrow_forwardA certain semiconductor device requires a tunneling probability of T=10^-5 for an electron tunneling through a rectangular barrier with a barrier height of Vo=0.4eV. The electron energy is 0.04eV. Determine the maximum barrier width.arrow_forwardIn a particular semiconductor device, electrons that are accelerated through a potential of 5 V attempt to tunnel through a barrier of width 0.8 nm and height 10 V. What is the tunneling probability through the barrier If the potential is zero outside * ?the barrier 1.02 x 10-8 2.26 x 10-8 4.5 x 10-8 16.4 x 10-8 1.13 x 10-8arrow_forward
- A thin solid barrier in the xy-plane has a 12.6µm diameter circular hole. An electron traveling in the z-direction with vx 0.00m/s passes through the hole. Afterward, within what range is vx likely to be?arrow_forwardAn electron is confined to move in the xy plane in a rectangle whose dimensions are Lx and Ly. That is, the electron is trapped in a two dimensional potential well having lengths of Lx and Ly. In this situation, the allowed energies of the electron depend on the quant numbers Nx and Ny, the allowed energies are given by E = H^2/8Me ( Nx^2/ Lx^2 + Ny^2/Ly^2) i) assuming Lx and Ly =L. Find the energies of the lowest for all energy levels of the electron ii) construct an energy level diagram for the electron and determine the energy difference between the second exited state and the ground state?arrow_forwardConsider a heat reservoir at temperature T is in contact with a one-dimensional quantum oscillator whose vibrational frequency is . Calculate the ratio of the probability of the oscillator that exists in the first excited state and to the ground state. Answer Choices: a. e b. e C. d. -(1) e no 2kgT e 2.000 32 Tarrow_forward
- True or false (a) Assume an electron's energy is measured with an uncertainty of leV, then the minimum uncertainty over the time is 2.7x10-16s. (b) For any given semiconductor material, electrons move(conduct) in valence. (c) In semiconductor we describe the movement of electrons as particle behavior (d) The position of an electron in an atom can be found preciselyarrow_forwardAn electron is trapped in a one-dimensional infinite potential well that is 200 pm wide; the electron is in its ground state. What is the probability that you can detect the electron in an interval of width öx = 5.0 pm centered at x = 100 pm? (Hint: The interval öx is so narrow that you can take the probability density to be constant within it.) Number i Unitsarrow_forwardElectron transfer between redox centers in proteins is controlled by quantum tunneling. We can model the region between two redox centers as an energy barrier which the electron must cross. If the distance between the redox centers is 0.752 nm and the energy of the electron is 0.976 eV lower than the height of the barrier, what is the probability that the electron will successfully cross to the next redox center?arrow_forward
- An electron is confined between two impenetrable walls 0.200nmapart. Determine the energy levels for the states n = 1,2 and 3.arrow_forwardConsider a three-level quantum system with a given energy levels E₁ = 0, E₂ = 1.0 x 10-23 J with a degeneracy of three and E3 = 3.10 x 10-23 J. Determine the probabilities for each energy levels if the heat bath has a temperature of 5 K.arrow_forwardAn electron is trapped in defect in a crystal lattice that is 10.0 A wide. Assuming you can approximate the defect as a one-dimensional infinite potential well, what would be the wave-length of the emitted photon as the electron falls from n = 3 to n = 2 quantum states?arrow_forward
 Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax


